Our Textbooks and Monographs
Let us introduce a textbook on advanced classical electrodynamics and a monograph on quantum electrodynamics.


Our Research
Quantum electrodynamics is a lot like baking a cake and then trying to take apart the individual ingredients. At least, that is what physicist Dr. Ulrich Jentschura equates to the process of creating an equation that can couple particles’ and antiparticles’ predicted masses at the same time.
“It is a little bit like trying to take an already baked cherry cake apart and separate its ingredients,” says Jentschura, a professor of physics at Missouri University of Science and Technology. “You can pick the cherries off the top, but you cannot separate the batter of egg, flour and sugar.”
With funding from the National Science Foundation, Jentschura and his research team are trying to “take apart” the Dirac equation, which describes particles and antiparticles simultaneously – antiparticles being the corresponding antimatter with the same mass and opposite charge of particles.
From: S&T physicist improves particle interaction modeling
– Peter Ehrhard
Quantum electrodynamics is a very developed field of study, with applications to the high-precision theory of atomic bound states, laser-matter interactions in the relativistic regime, and, on the low-energy side, the description of dynamic processes involving atoms and the quantized electromagnetic field.
In the following, an overview is given of the most important subfields of study, which have been given attention over the last years. However, the list given below does not include some recent development. Indeed, branching out from quantum electrodynamics of bound states, investigations have been carried out in the field of relativistic quantum mechanics and general relativity, atomic interaction and dynamic processes, quantum field theory of bound states, particle physics, and heavy-ion collision, and theoretical relativistic laser physics, work specifically connected with the determination of fundamental constants, as well as publications on the renormalization group and large-order perturbation theory. Exotic areas like the physics of sports and some considerations on numerical algorithm development complete the picture.
Recent developments include a comprehensive account of gravitational effects in the spectra of bound systems, and limitations of Einstein’s equivalence principle, given here, the analysis of atomic physics constraints on new particle models (see research article), and the identification of long-range tails in van der Waals interactions (see here). In general, the fields of interest have branched out a little more toward general relativity, in recent years, and borderline areas toward atomic physics. Probably, the most important result obtained in recent years concerns the equivalence principle for antiparticles, which has been investigated and, perhaps, conclusively demonstrated here. Furthermore, problems connected to the interaction of atoms, including those in metastable states, with surfaces (see our research article), have been considered. Quantum electrodynamics is sometimes characterized as a theory that describes somewhat exotic effects, tiny corrections which are important mainly for high-precision experiments. This is not the case, as shown in recent works. The quantum theory of blackbody and non-contact van der Waals friction, which is important for astrophysical processes, has been considered here. The surprising conclusion is that the so-called one-loop quantum electrodynamic “correction” in this case dominates over the tree-level term.
A further example where insight into quantum electrodynamic processes is crucial for the analysis of dynamic processes involving bound states concerns two-photon decays from highly excited states. The problem is that in typical cases, virtual states of lower energy than the decaying state, but higher energy than the ground state, exist which can be reached via a dipole transition. One thus has to separate the coherent contribution to the two-photon decay rate, from the sequential one-photon transition via the intermediate (virtual state). The latter process is also known as a cascade. This problem has been addressed in a number of publications, including this one and here, following an initial account given as a fast-track communication.
QED and Bound Spectra
The quantum electrodynamic theory of bound states started with the observation of the 2S-2P energy level splitting in atomic hydrogen (Lamb shift). Bound-state quantum electrodynamics uses concepts from relativistic atomic physics and quantum field theory. For more than fifty years, generations of theoreticians and experimentalists have been improving both our theoretical understanding as well as the laser-spectroscopic experimental techniques, and today’s highly sophisticated calculations would be impossible without the extensive use of computer algebra systems and parallel computers.
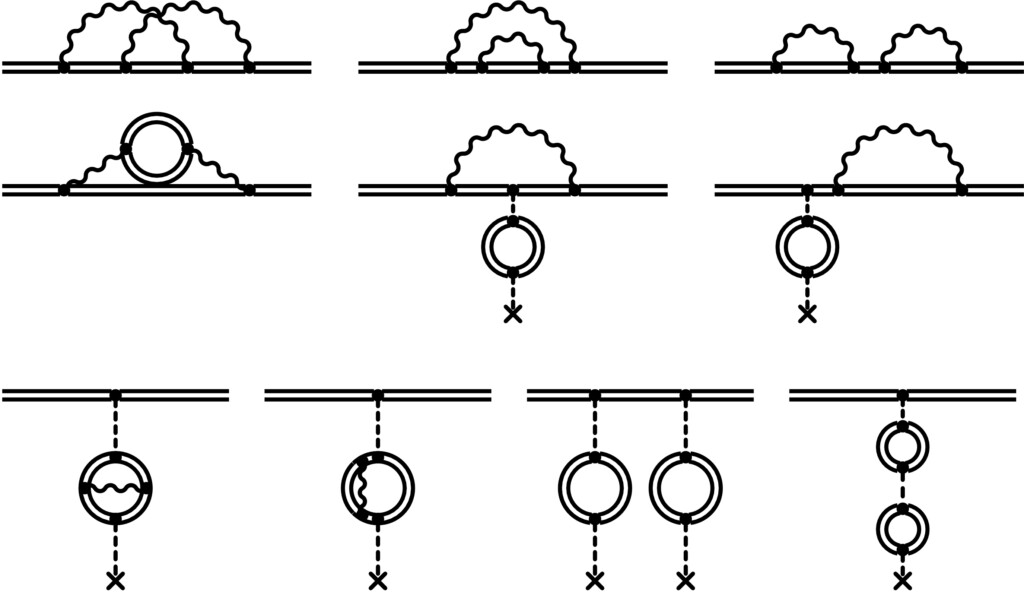
Figure 1: Two-loop corrections to the Lamb shift (Feynman diagrams).
Among the subjects studied by the group are two-loop Bethe logarithms [1] higher-order two-loop effects for excited states [2], and, together with scientists from the National Institute of Standards and Technology, quantum electrodynamic effects for highly excited Rydberg states [3]. A procedure to infer fundamental constants from spectroscopic data is described in Ref. [3]. Fundamental predictive limits of quantum electrodynamics now become relevant for the description of experiments, which gives rise to a very interesting situation [5]. In view of the recently observed discrepancy of theory and experiment in muonic hydrogen (the so-called muonic hydrogen puzzle, see Ref. [5]), the spectrum of muonic hydrogen has been re-analyzed [6] and possible physical explanations have been discussed [7].
One should briefly comment on magnetic interactions in atoms. Traditionally, the calculation of the transition energies among hyperfine centroid frequencies has been emphasized. The nuclear-spin dependence of the level energies leads to the hyperfine splitting (for a nonperturbative calculation of the QED correction to hyperfine splitting, see Ref. [8]). The bound-electron g factor is important for the determination of the electron mass. Two-loop corrections to the bound-electron g factor (for 1S and 2S states) have also been investigated, in addition to the Lamb shift, and complete results have been obtained for a term of order α (Z α)4 ln[(Z α)-2], which contributes to the ratio of the electronic Larmor precession frequency and the cyclotron frequency of a hydrogenlike ion in a trap [9,10]. The result improves the electron mass determination from the carbon and oxygen ion measurements [11].
[1] K. Pachucki and U. D. Jentschura, Phys. Rev. Lett. 91, 113005 (2003).
[2] U. D. Jentschura, Phys. Rev. A 74, 062517 (2006).
[3] U. D. Jentschura, P. J. Mohr, J. N. Tan, B. J. Wundt, Phys. Rev. Lett. 100, 160404 (2008).
[4] U. D. Jentschura, S. Kotochigova, E.-O. Le Bigot, P. J. Mohr and B. N. Taylor, Phys. Rev. Lett. 95, 163003 (2005).
[5] R. Pohl et al., Nature 466, 213 (2010)
[6] U. D. Jentschura, Ann. Phys. (N.Y.) 326, 500 (2011)
[7] U. D. Jentschura, Ann. Phys. (N.Y.) 326, 516 (2011)
[8] V. A. Yerokhin and U. D. Jentschura, Phys. Rev. Lett. 100, 163001 (2008).
[9] K. Pachucki, A. Czarnecki, U. D. Jentschura and V. A. Yerokhin, Phys. Rev. A 72, 022108 (2005).
[10] J. Verdu et al., Phys. Rev. Lett. 92, 093002 (2004).
High-Intensity Lasers and the Furry-Volkov Picture
For a tightly bound electron (close to a high-Z nucleus), the so-called Furry picture provides for a suitable description: one integrates the Coulomb interaction into the unperturbed Hamiltonian and formulates the field operator for the Dirac field in terms of bound and continuum states of the Dirac-Coulomb problem. Today’s high-intensity lasers are so intense that proverbially, “matter perturbs light” whereas otherwise “light perturbs matter.” This situation means that the external, dressing, laser field needs to be incorporated into the unperturbed Hamiltonian. A further complication arises: One would like to calculate S-matrix elements, which necessitates the expansion of the propagators into plane waves of the form exp(ip.x), and therefore, gives rise to so-called generalized Bessel functions which are infinite sums of ordinary Bessel functions and have proven to be notoriously difficult to evaluate.
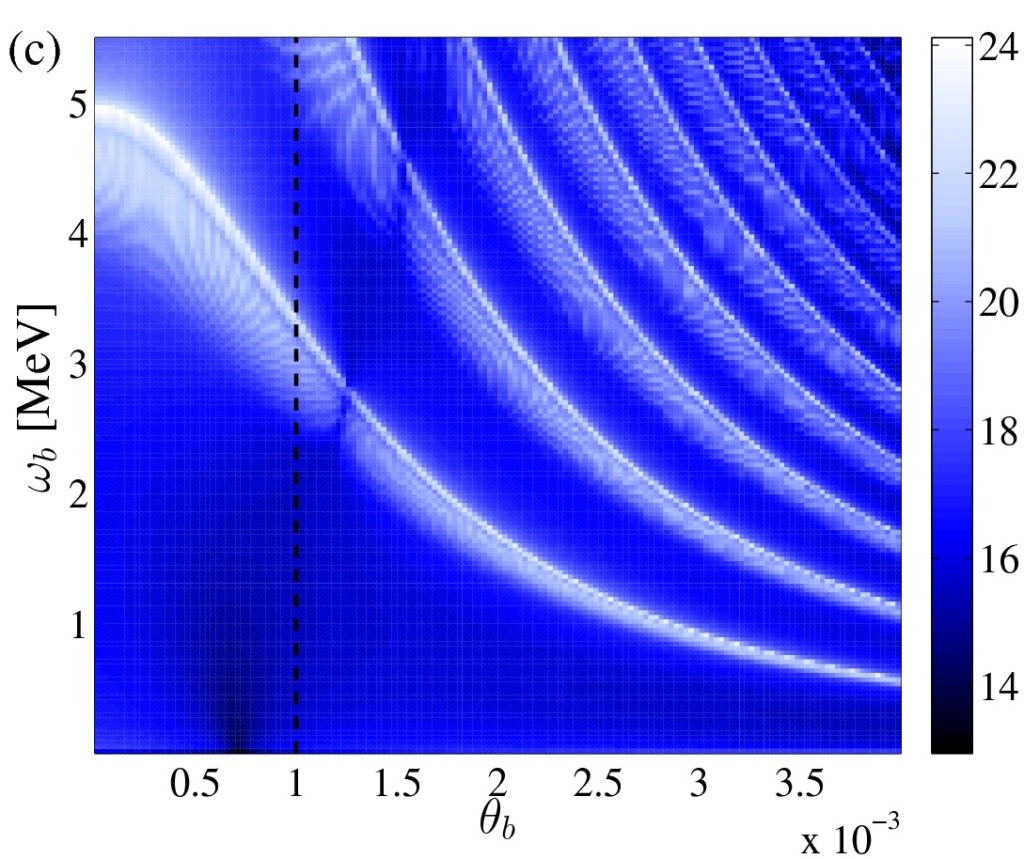
Figure 2: Double Compon backscattering in an intense laser field. The maximum of the scattered photon energy is reached for direct backscattering, at θb=0. For nonvanishing θb, the energy of the scattered photon decreases, but multi-photon absorption processes from the laser field lead to higher harmonics of the one-photon Compton scattering process.
The Dirac-Volkov propagator in the Furry picture with respect to a plane-wave laser field has been written down in Ref. [11]. The calculation of generalized Bessel functions with the help of recursion relations has been described in Ref. [12]. A number of physical processes have been calculated using the Dirac-Volkov propagator. These include the double Compton scattering in a laser field (see Figure 2), where an electron undergoes a transition from one Dirac-Volkov state to another Dirac-Volkov state, emitting a correlated pair of photons [13].
[11] S. Schnez, E. Lotstedt, U. D. Jentschura, C. H. Keitel, Phys. Rev. A 75, 053412 (2007).
[12] E. Lötstedt, U. D. Jentschura, Phys. Rev. E 79, 026707 (2009)
[13] E. Lötstedt, U. D. Jentschura, Phys. Rev. Lett. 103, 110404 (2009).
Novel States of the Light Field
Novel states of the light field called “twisted photons” are rather interesting objects. The electromagnetic vector potential describing a twisted photon state adds the orbital angular momentum of the photon to the spin angular momentum of the vector (spin-1) field. In some sense, the twisted wave function interpolates between a plane-wave vector potential and a photon described by a vector spherical harmonic (in the standard multipole decomposition). Indeed, a plane-wave photon whose vector potential describes a photon propagating in a specific direction, say, the z direction. It has zero expectation value for the projection of the orbital angular momentum onto the propagation axis (z axis). A photon described by a vector spherical harmonic has defined values for the square of the angular momenta but does not have a defined propagation direction.
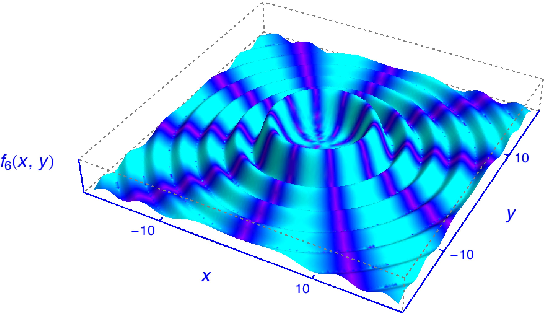
Figure 3: Wave function of a twisted photon with a phase of the vector potential component being indicated by color grading.
Twisted photons combine, in some sense, the properties of plane-wave photons and those described by vector spherical harmonics: Namely, they have a defined propagation direction (say, the z axis) and still, large angular momentum projections onto that same propagation axis. In constructing vector spherical harmonics, one adds the orbital angular momentum from the spherical harmonics to the spin angular momentum, using Clebsch–Gordan coefficients. However, one can also add the orbital angular momentum to the spin angular momentum via a conical momentum spread (in momentum space) multiplied by an angle-dependent phase, or by a Bessel function in the radial variable (in coordinate space). This leads to twisted states.
Figure 3 shows a plot of a twisted photon vector field. The rainbow-scale color variation of this potential indicates complex phases, which are superpositions of terms proportional to the azimuthal angle of the transverse momentum. The frequency upconversion of twisted photons by Compton backscattering discussed in Ref. [14,15] should open new experimental possibilities for fundamental studies in atomic and nuclear physics.
[14] U. D. Jentschura, V. G. Serbo, Phys. Rev. Lett. 106, 013001 (2011).
[15] U. D. Jentschura, V. G. Serbo, Eur. Phys. J. C 71, 1571 (2011).
Generalized Nonanalytic Expansions
Normally, physiscists think in terms of power series when they want to describe a physical phenomenon. A proverb probably invented by graduate studies is that during graduate school, one learns that every formula investigated during undergraduate studies is nothing but the start of a Taylor series. A classical quantum-mechanical problem consists in a harmonic oscillator perturbed by a quartic term (anharmonic oscillator). The perturbation is of the form g q4, where g is the coupling, and q is the coordinate. A perturbation series for the energy of a typical state, expressed in powers of the coupling g, diverges factorially in higher order no matter how small g is. Indeed, this remarkable phenomenon is intimately connected with the fact that for g < 0, the perturbation g q4 actually is unstable, and the resonance energies become complex. Conversely, in the path integral representation of the partition function, one finds nontrivial saddle points, which correspond to instanton trajectories of a classical particle travelling between the maxima the inverted potential (see Figure 4).
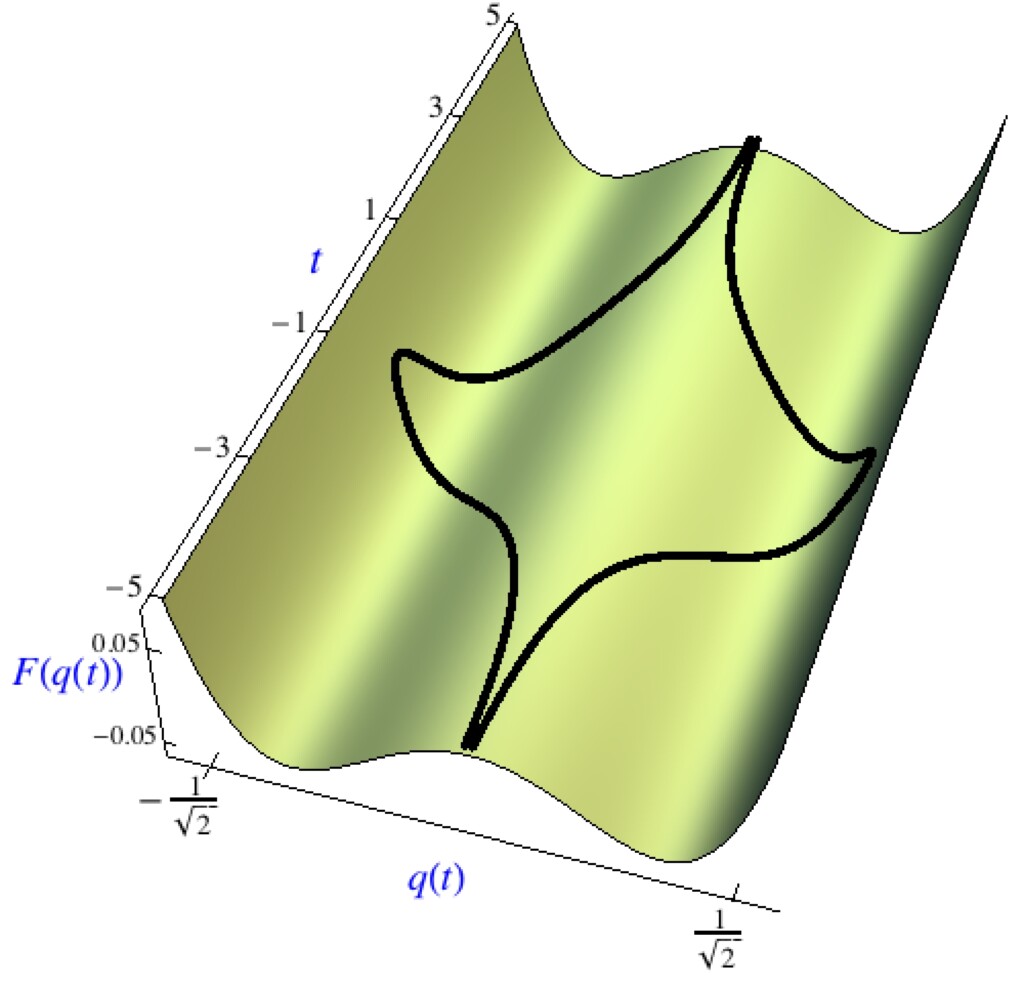
Figure 4: Instanton configurations in an inverted quartic potential for negative coupling. The particle starts at the central maximum and travels either to the right or to the left, before making its way back to the central maximum.
Using an expansion about the nontrivial saddle points of the Euclidean action, one can then derive a few interesting higher-order formulas, and verify these against high-precision numerical calculations. Eventually, it has been found that a complete description of the resonance energies of anharmonic oscillators requires a fundamental generalization of the concept of a power series in the coupling parameter g: namely, one has to allow for powers, logarithms, and nonperturbative exponentials exp(-A/g) of the coupling parameter, where A is the instanton action. Generalized nonanlytic expansions, that involve all the mentioned expressions, have been used for high-precision numerical evaluations [16,17,18], and also, for the test of generalized Bender-Wu formulas that have been derived for odd anharmonic oscillators [19].
[16] J. Zinn-Justin, U. D. Jentschura, Ann. Phys. (N.Y.) 313, 197 (2004).
[17] J. Zinn-Justin, U. D. Jentschura, Ann. Phys. (N.Y.) 313, 269 (2004).
[18] U. D. Jentschura, J. Zinn-Justin, Phys. Lett. B 596, 138 (2004).
[19] U. D. Jentschura, J. Zinn-Justin, Phys. Rev. Lett. 102, 011601 (2004).
Renormalization Group and Critical Phenomena
The idea of the renormalization-group (RG) theory was born when Gell-Mann and Low observed that the shape of the vacuum-polarization induced charge distribution about a particle, for small distances, does not depend on the mass of the screening quantum field. Due to the vacuum-polarization effect, the effective charge felt by a probing particle depends on the distance from the “bare” charge of the screened particle (the coupling “runs”). Because the shape of the vacuum-polarization charge distribution is virtually independent of the mass of the screening virtual quantum field, the rate of “running” of the coupling is a function of the particular value of the coupling itself, at a particular distance: It is thus possible to formulate a so-called ψ=ψ(g) function which describes the running of the coupling. Due to the Ward-Takahashi identity, it is possible to isolate the running of the coupling from the wave function and mass renormalizations in QED.
If one uses the approach for general field theories, the calculations become more complex: One has to formulate the RG for an arbitrary Green function [or a one-particle irreducible (1PI) generating functional], including wave function (field) renormalizations. The field renormalizations describe the behaviour of the Green functions at large distances. Near a fixed point of the RG transformation, they describe the “anomalous” exponent of the correlation function that describes its variation with distance. The mathematical form of the correlation differs from a simple integer power law. Therefore, the RG functions describing the wave function renormalizations are called the “anomalous dimensions.” These quantities are relevant for the description of, e.g., O(N)-symmetric φ4 theories. The universality classes of these theories are important for a number of observed second-order phase transitions at low, but finite temperature, such as the liquid-vapour transition of 3He or the superfluid transition of 4He. The Euclidean actions of these theories have the same structure as those used for the anharmonic oscillators, and possible connections may be explored.
Theories with periodic self-interactions cannot be renormalized in the perturbative approach that is available for O(N)-symmetric φ4 theories. In a series of papers [20-23], we have analyzed the O(N)-symmetric theories with interaction terms of the form cos(b.φ), with a special emphasis on two spatial dimensions (2D sine-Gordon model). The interaction contains terms of arbitrarily high power in the field variable, as a result of the expansion of the periodic cosine term. The two-dimensional sine-Gordon model undergoes a phase transition (the Kosterlitz-Thouless-Berezinskii phase transition) which is characterized by the binding/unbinding of topological excitations (vortices). It belongs to the same universality class as the 2D XY model and the 2D Coulomb gas. Vortices are free above the critical temperature (negative free energy), whereas they are bound below the critical temperature. The Wegner-Houghton equation has been used in order to infer the renormalization-group flow of the models [20]. The critical value for the b parameter characterizing the transition was identified and compared within various blocking schemes that integrate the momentum shells in the Polchinski and Wegner-Houghton approaches.
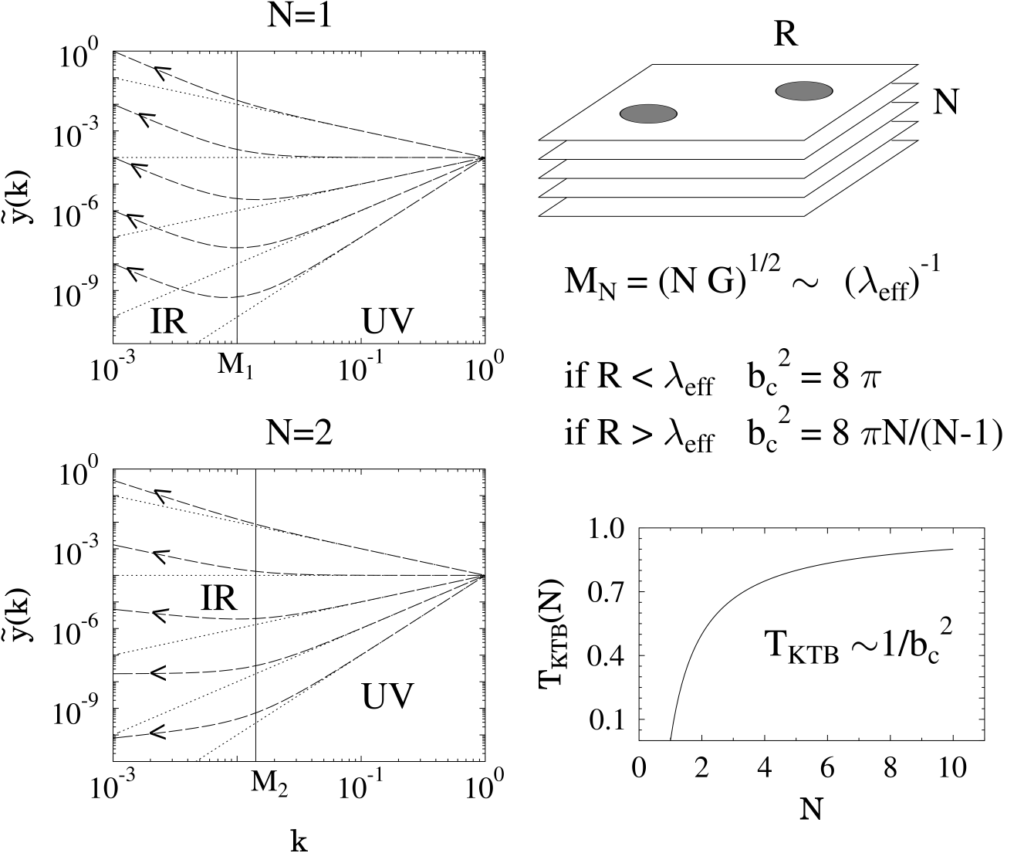
Figure 5: RG flow of the coupling in a layered sine-Gordon model. The coupling becomes relevant/irrelevant in the infrared depending on the temperature parameter bc. The critical value of bc depends on the number N of superconducting layers.
In high-temperature superconductors, it is generally assumed that the conduction proceeds by the formation of tightly bound vortices. The layered crystal structure of the high-temperature superconductors suggests that it might be indicated to invoke a layered sine-Gordon model, where the different layers are coupled by interaction terms. The layer-dependence of the interaction was first analyzed in [20]. We have found that for N magnetically coupled layers, the transition temperature varies as [1 – 1/N] with the number of layers [22,23]. A field-theoretical analysis has been presented in Ref. [21]. The theory of phase transitions in two-dimensional systems seems to be not very well developed, and it has even been a considerable challenge to identify the parameters of the model with the physical quantities such as the transition temperature. The papers [22,23] seem to attract attention within the solid-state physics community after an initial period of neglect.
[20] I. Nandori, S. Nagy, K. Sailer, U. D. Jentschura, Nucl. Phys. B 725, 467 (2005).
[21] U. D. Jentschura, I. Nandori, J. Zinn-Justin, Ann. Phys. (N.Y.) 321, 2647 (2006).
[22] I. Nandori, U. D. Jentschura, S. Nagy, K. Sailer, K. Vad, S. Meszaros, J. Phys.: Condens. Matter 19, 236226 (2007).
[23] I. Nandori, K. Vad, S. Meszaros, U. D. Jentschura, S. Nagy, K. Sailer, J. Phys.: Condens. Matter 19, 496211 (2007).
Lamb Shift in Laser Fields
The combination and unification of ideas from intense-field quantum optics and quantum electrodynamics demands a thorough analysis of the interplay of the strong driving of an atom by a laser field (Rabi oscillations) and the vacuum fluctuations. In [24,25], an atom with two relevant energy levels driven by a strong near-resonant monochromatic laser field is studied as the easiest model system for the above problem.
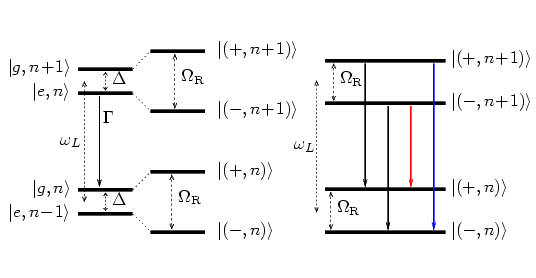
Figure 6: Schematic diagram (left) showing the coupling of the bare atomic states and the Fock states to the laser-dressed states. The transitions among the dressed states, shown in the right figure, lead to the red- and blue-detuned Mollow sideband peaks.
As is well known within quantum optics, the incoherent part of the resonance fluorescence spectrum emitted by this system is known as the Mollow spectrum. The atom-laser coupling strength is characterized by the Rabi frequency which is proportional to the product of the transition dipole matrix element and the laser field strength. In steady state, the system is described by quasi-energy eigenstates known as the laser-dressed states which are shown in Figure 6. They are displaced from the bare atomic states by one half of the generalized Rabi frequency ΩR = (Ω2 + Δ2)1/2, where Ω is the Rabi frequency and Δ is the detuning. The incoherent spectrum generated by the many-photon processes, in steady state, can then be interpreted in a natural way in terms of transitions among the laser-dressed states.

Figure 7: The self energy of a laser-dressed bound electron (Feynman diagram, left figure) shifts the incoherent fluorescence spectrum (known as the Mollow spectrum) from the black to the red curve (right figure). The electron propagator in the left figure is actually double-dressed, (i) by the Coulomb field of the nucleus (as indicated by the double line, and (ii) by the laser field which is indicated by a wavy line. The zero on the abscissa of the right figure is fixed to the laser frequency. The ordinate axis gives the intensity distribution of the incoherent spectrum (in arbitrary units).
When evaluating radiative and relativistic corrections to the Mollow spectrum, it is natural to start the analysis from the dressed-state basis as opposed to the unperturbed atomic bare-state basis. At nonvanishing detuning and nonvanishing Rabi frequency, a treatment starting from the dressed-state basis leads to additional correction terms, which may be summarized in a modified Mollow sideband formula (see Figure 7) including relativistic and radiative corrections, which entails both a modification of the Rabi frequency as well as a correction to the transition dipole moment. The corrections to the Rabi frequency include some nontrivial effects which can only be understood if the problem is treated right from the start in the dressed-state basis, apart from relativistic and radiative corrections to the transition dipole moment, field-configuration dependent corrections, higher-order corrections to the self-energy, and corrections to the secular approximation. The corrections to the detuning comprise the bare Lamb shift, Bloch-Siegert shifts, and off-resonant radiative corrections. All of these effects are described in detail in [13], and a schematic view of their consequence for the Mollow spectrum is given in Figure 7.

